SVD

SVD (Singular Value Decomposition) is one of my favorite topics in linear algebra. It's almost magical to factorize any matrix into a product of two orthogonal matrices and a diagonal matrix.

Derivation

In simple words, any matrix 'A' can be decomposed into a product of 3 matrices : U, ∑ and V, where ∑ contains the singular values along it's diagonal, and U & V are unitary matrices. Here is a derivation for SVD

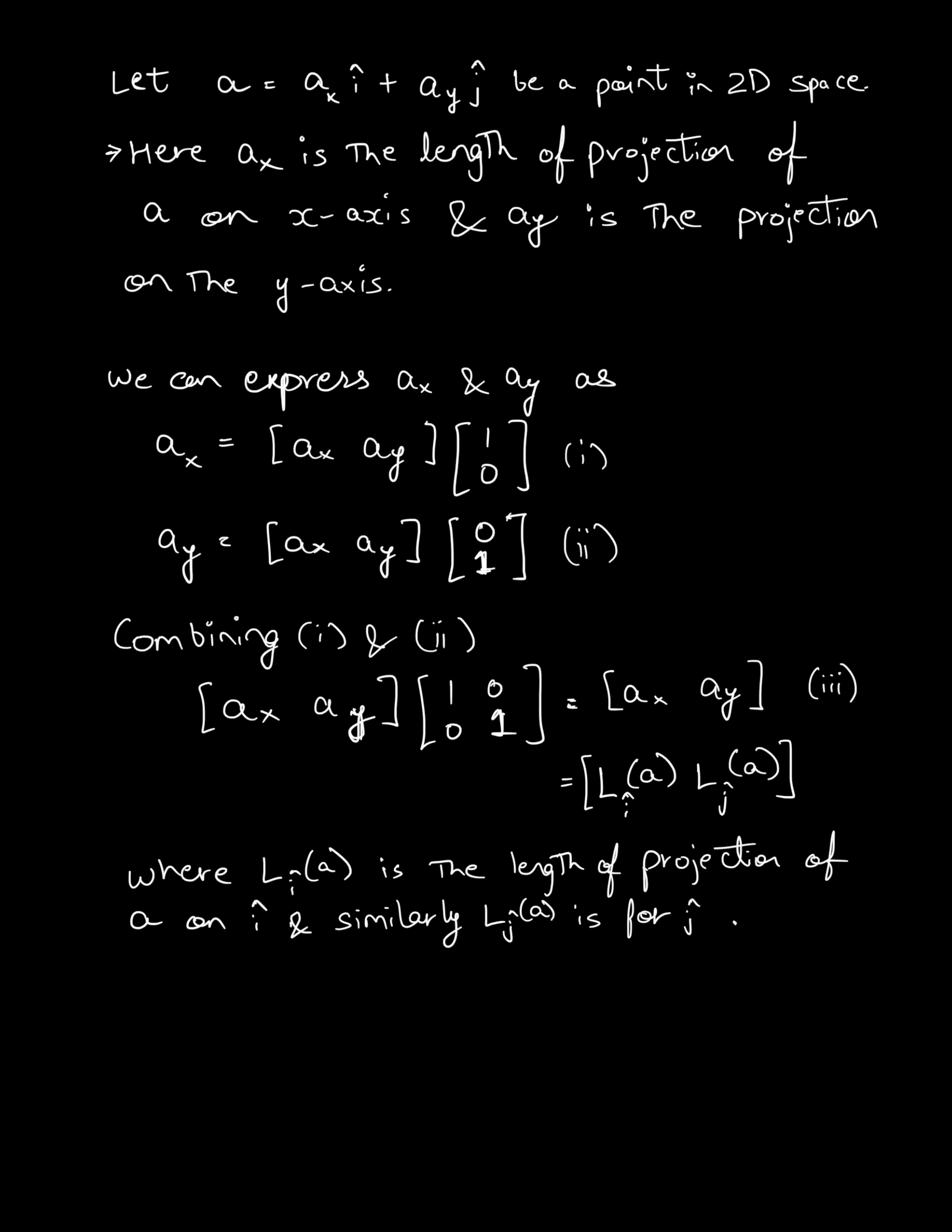
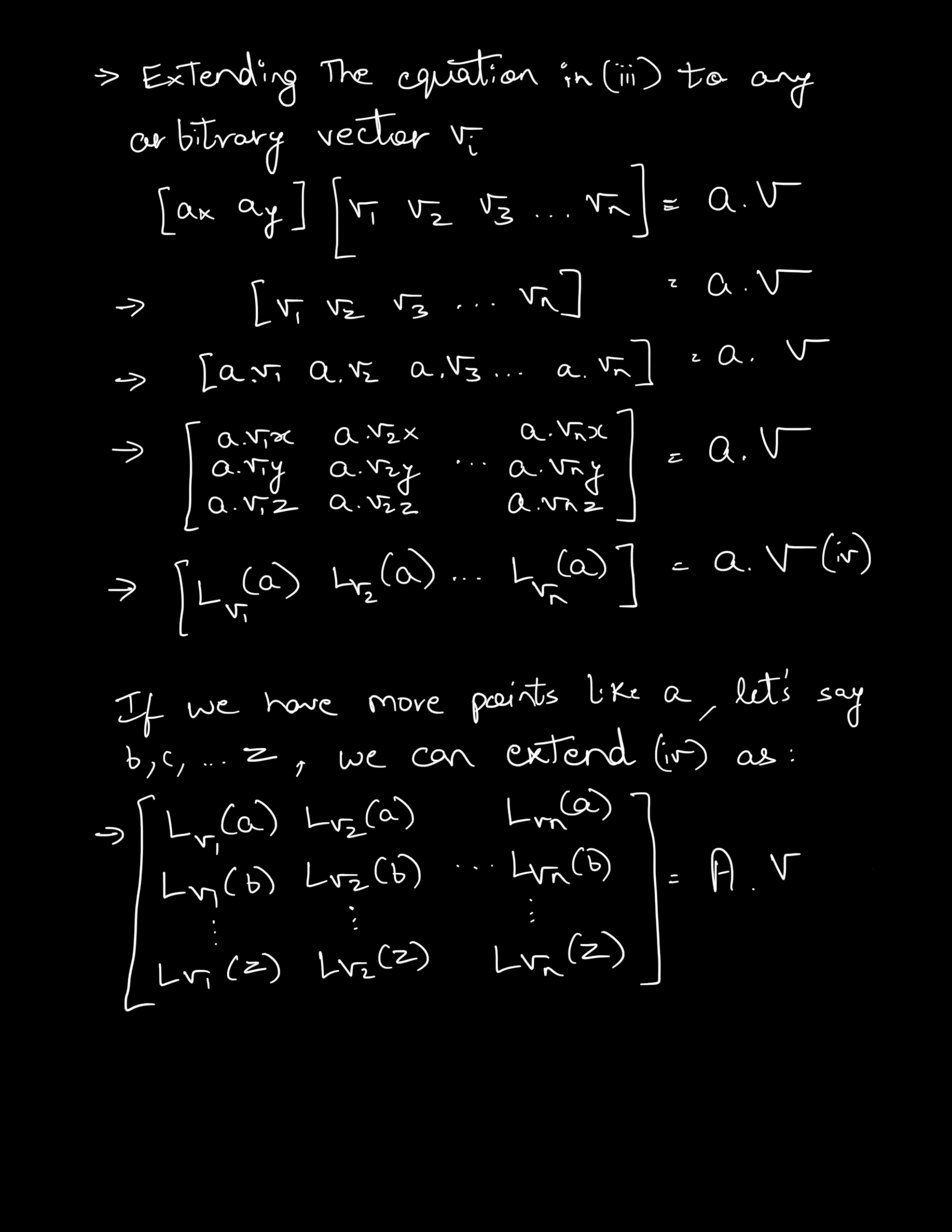
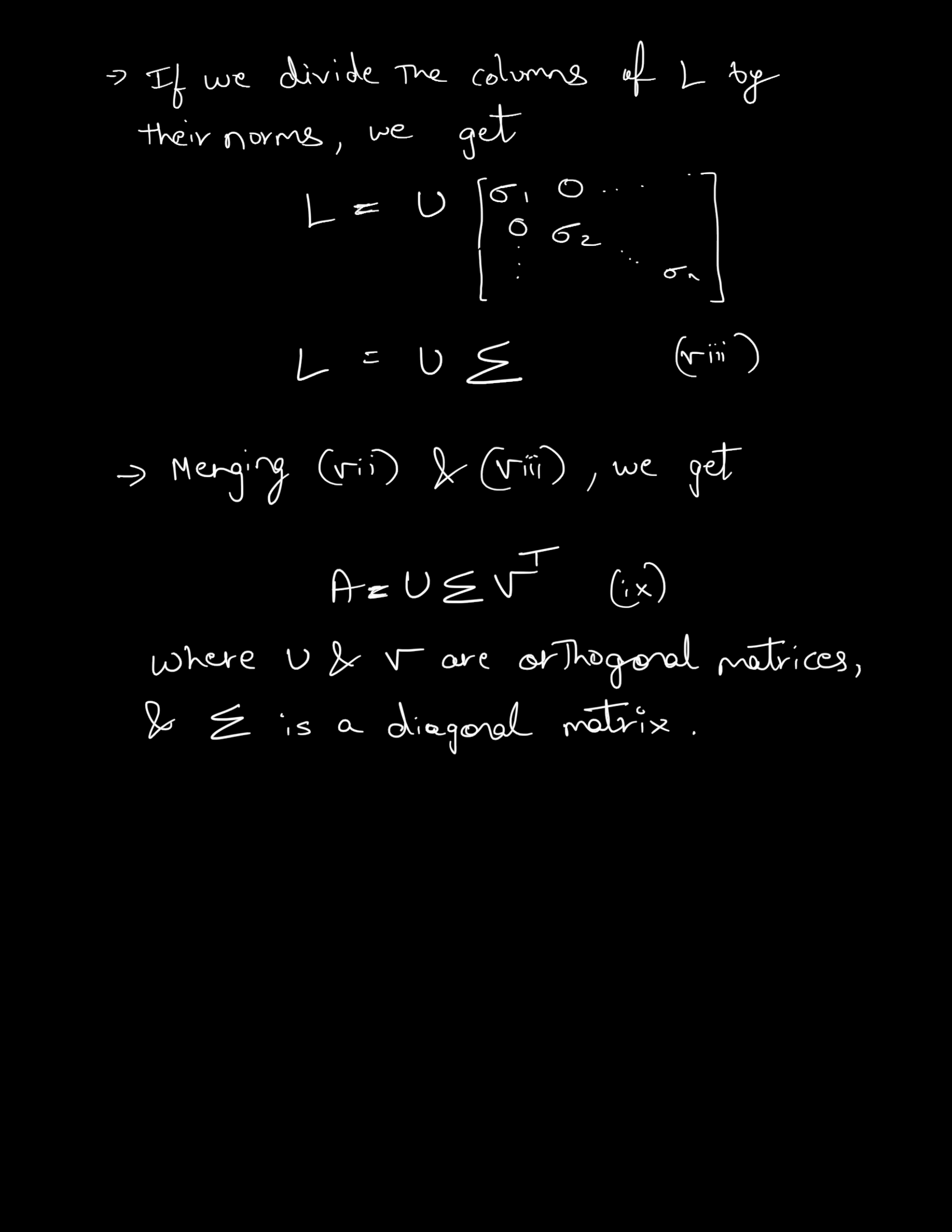
Applications

1. Image compression
2. Low-rank approximations
3. PCA
4. Rank determination
5. Least squares

and a million more...

Let's look at one such application in computer vision:

Image compression

What if we delete small singular values from ∑ and its corresponding vectors from U and V ? We can then obtain the projection of A onto a lower-dimensional subspace. This technique can be used to compress an image at the loss of some high-frequency information.

Using this code, we can reconstruct the image using the first N components

from PIL import Image 
import numpy as np \
import matplotlib.pyplot as plt

img = Image.open('tiger.webp') img = np.array(img) gray = 0.2989 * img[:, :, 0] + 0.5870 * img[:, :, 1] + 0.1140 * img[:, :, 2]

U,s,V = np.linalg.svd(gray)

recon_imgs=[] for n in [5, 15, 30]: S = np.zeros(np.shape(gray)) for i in range(0, n): S[i,i] = s[i] recon_img = U @ S @ V recon_imgs.append(recon_img)

fig, ax = plt.subplots(2, 2)

ax[0][0].imshow(gray, cmap='gray') ax[0][0].axis('off') ax[0][0].set_title('Original')

ax[0][1].imshow(recon_imgs[0], cmap='gray') ax[0][1].axis('off') ax[0][1].set_title(f'Reconstructed n = 5')

ax[1][0].imshow(recon_imgs[1], cmap='gray') ax[1][0].axis('off') ax[1][0].set_title(f'Reconstructed n = 15')

ax[1][1].imshow(recon_imgs[2], cmap='gray') ax[1][1].axis('off') ax[1][1].set_title(f'Reconstructed n = 30') 
plt.show()

There are 942 singular values for the original image, since it's a (942x942) image with unique pixel rows.

We can recover most of the low-frequency information from the image using only the first 15-30 components of SVD. Even the finer details like eyeballs are present in the reconstructed image, with a compression rate of ~ 2000-4000.